Palindrome

DP

팰린드롬? 문제에서 사용할 수 있는 기법이다.

코드를 보면 점화식을 바로 이해할 수 있다.

코드

int arr[2001];
bool dp[2002][2002];

int main()
{
	int n, m;
	cin >> n;
	for (int i = 0; i < n; i++)
		cin >> arr[i];

	for (int i = 0; i < n; i++)
	{
		dp[i][i] = 1;
		dp[i][i + 1] = 1;
	}

	for (int len = 2; len <= n; len += 1)
		for (int i = 0; i <= n-len; i++)
			dp[i][i + len] = dp[i+1][i + len - 1] && arr[i] == arr[i + len - 1];


	cin >> m;
	while (m--)
	{
		int s, e;
		cin >> s >> e; s--; e--;
		cout << (dp[s][e + 1] ? 1 : 0) << '\n';
	}
}

Manacher’s Algorithms

이 글을 쓰게된 이유이다. 블로그에 설명이 정말 잘 되어있으나, 내가 바로 이해하기엔 글이 압축적이어서 여기에 풀어 적는다.

설명

코드

const int MAXIN = 2501;
char in[MAXIN * 2]; int n;
int dp[MAXIN*2];

void Manacher()
{
	int r = 0, p = 0;
	for(int i = 0; i < n; i++)
	{
		if (i <= r)
			dp[i] = min(dp[p * 2 - i], r - i);
		else 
			dp[i] = 0;

        // i 를 중심으로 가능한 팰린드롬의 반지름을 하나씩 비교하며 계산
		while (i - dp[i] - 1 >= 0 && i + dp[i] + 1 < n && in[i - dp[i] - 1] == in[i + dp[i] + 1])
			dp[i]++;  

        // 기준 팰린드롬 업데이트
		if (r < i + dp[i])
		{
			r = i + dp[i];
			p = i;
		}
	}
}

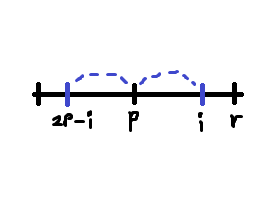
변수의 의미를 먼저 정의를 하자. dp[i] 는 i 를 중심으로 한 팰린드롬의 반지름이다. r 은 현재 구한 펠린드롬의 끝부분의 인덱스 중 최댓값이다.p 는 기준 팰린드롬의 중심 인덱스로 r 이 업데이트 될 때 같이 바뀐다.

원리는 펠린드롬의 대칭성을 이용하는 것이다.

위 그림에서 p 를 중심으로 오른쪽으로는 r 까지 문자열이 대칭된다고 하자. 임의의 인덱스 i 는 단순한 산수를 해보면 p 를 중심으로 2p-i 와 대칭된다. 그러면 i 를 중심으로 하는 펠린드롬은 2p-i 를 중심으로 한 펠린드롬과 관계가 있음을 알 수 있다.

• 이때 2p-i 를 중심으로 한 팰린드롬이 기준 팰린드롬을 벗어나면 대칭성을 이용할 수 없다. 그래서 범위 내의 최대의 길이가 되는 r-i 와 min() 를 해줘야 한다.
• 그래서 min(r-i, dp[2p-i]) 는 팰린드롬을 이용해 보장된 팰린드롬의 최소반지름이 된다.

이제 두가지 경우로 나눌 수 있다.

• i + 최소반지름 < r. 그러면 대칭성으로 인해 최소반지름은 반지름과 같아진다. 그래서 비교를 할 필요가 없다.
• i + 최소반지름 == r. 그러면 팰린드롬의 반지름은 우리가 구한 최소반지름보다 여지가 있다. 그래서 위 코드의 while() 문을 통해 실제 반지름을 구할 수 있다. 이 팰린드롬은 다시 기준 팰린드롬이 된다.

우리가 while() 문에서 비교하는 문자는 r 번째 문자부터 이어서 시작한다. 그러므로 전체 시간복잡도는 O(\(\mathrm{N}\)) 이 된다.

짝수 팰린드롬

위 방법은 홀수 팰린드롬만 구할 수 있다. 짝수 팰린드롬은 문자열 사이사이에 유니크한 문자를 삽입하면 처리할 수 있다. 대략 다음 코드처럼 처리하면 된다.

    scanf("%s", in); n = strlen(in);
    for (int i = n-1; i >= 0; i--) in[(i<<1)+1] = in[i];
    for (int i = 0; i <= n; i++) in[i<<1] = '#';
    n = n * 2 + 1;

이때 일정범위 내가 팰린드롬인지는 구하는 코드는 다음과 같다.

// s, e 는 특수문자 삽입 전 인덱스
//(s*2+1 + e*2+1) / 2
inline bool Chk(int s, int e)
{
	return s == e || dp[s + e-1] >= e - s-1;
}